Large-Scale Load Stabilization

by Margarita Dzhalalova
       There is an economic necessity in certain cases of large-scale load transfer (e.g., dwelling houses, industrial pipes, etc.) by helicopters over long distances sometimes. Very often a stabilization problem of two connected bodies mechanical systems in airflow appears. Cases of a load swinging are known when a helicopter develops a speed of 80-100 km per hour  (however a helicopter has a capacity of going three times as fast). For stabilization of towed loads different hinge-fairings are used. One may use parachute systems for such purposes. One part of a parachute application project between Moscow State University and Academy of Civil Aviation (Saint-Petersburg) for stabilization of poorly-streamlined loads is considered in this article.
Results of experimental and numerical investigations of a permeable round parachute with the stripe-stabilizer, the so called "SAL" parachute - Stabilization of Aerodynamic Loads, are given [1].
       Experimental investigations of a round parachute model with an additional stripe for stabilization have been carried out in the Grand Aerodynamic Wind Tunnel at the Institute of Mechanics of the Moscow State University. This parachute model was designed with 24-triangular gores manufactured of sections cut from woven parachute cloth of air- permeability parameter l about 800 l/m2s with a vent and sewed stripe for stabilization (so called stripe-stabilizer) on the suspension lines (in the same plane), on a short distance from a canopy edge.
       The model has the following parameters: a number of suspension lines - 24, the vent radius –26 cm, length distance between canopy edge and stripe-stabilizer – 13 cm, stripe width – 28 cm, length of lines –175 cm, the total length of reefing cord, passed through the middle of a stripe, D0= 426 cm.  Nine various stages of reefing have been considered in the course of the tests: (cord of reefing was being shortened up to length D with a step of 30 cm). For each reefed parachute variant all loads were being measured at the confluence point at air flow velocities V= 10, 15, 20, 25, 30, 35 m/s. The parachute canopy attained different shapes from each other depending on the value of reefing (Fig.1).
D1=0.366, v=25 m/s: D6=0.718, v=35 m/s; D9=0.96, v=30m/s
Fig.1 Parachute model in Grand Aerodynamic Wind Tunnel. Numbers of the reefing 1, 6 and 9.

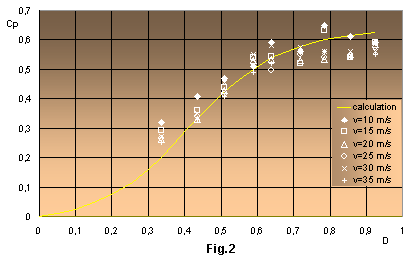
       In Fig.2 values of a drag coefficient are represented by different experimental symbols according to the upstream flow velocity via various parameters of reefing D = Dp/D0. Drag coefficient Cp = F/(rv2/2)S  is related to a canopy surface area without stripe-stabilizer area, where F is the aerodynamic load, acting on the canopy, q = rv2/2 is aerodynamic pressure of the upstream flow,  S is the total area of the main canopy. Values D corresponding to numbers of reefing variants: D = 0.366 corresponds to number 1; D = 0.47 - to number 2;…, D = 0.93 - to number 9.

Values of drag coefficient Cp depending on the parameters of reefing
       Stable balance of the parachute in the flow should be specially noted: angle oscillations exceeding a common pulsations were not discovered. Little vibrations of suspension lines and the canopy edge were observed at all values of upstream flow velocities and reefing, but the parachute itself kept a stable position (parachute axis pole-confluence point was parallel to the vector of the airflow).
As given below some numerical investigations of the stripe-stabilizer reefing influence on the canopy shape, its aerodynamic drag and the tension of radial ribbons are considered.
       The system of differential equations for the solution of this problem conformably to the considered parachute model was used [2]. This system describes the equilibrium of any radial ribbon element of a round parachute canopy:
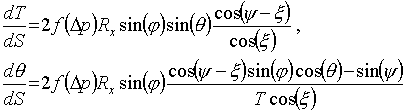    (1)
       To obtain the solution of this system, Cartesian coordinate system has been chosen, with the origin on the pole. The canopy axis is directed along ordinate axis Or, axis OR is perpendicular to Or (Fig.3). To determine the point's coordinates on the radial ribbon of inflated canopy this system is complemented by two more equations
   (2)
Scheme of one parachute gore
where T is a tension of the radial ribbon; S is a coordinate along the radial ribbon from the pole to the edge; q is the angle between tangent, plotted to meridional section, and the canopy axis;  Rx is the radius curvature of the canopy element, stretched between the neighbouring radial ribbons based on the angle 2f.  Rx is in the plane of normals, the angle between them is x.  There is a complete system of differential equations (1) and (2) with unknown T, q, R, r and the following boundary conditions of the problem:
at the coordinate origin, i.e. on the canopy pole, tangent to meridional section is perpendicular to canopy axis. Therefore q(0) = p/2; R(0) = 0, r(0) = 0, but the value of tension  T(0) on the pole is unknown.  On the canopy edge the tangent coincides with suspension lines, i.e.
    Lsin(q) + R = 0,   (3)
where L is the given line length, R is the distance between the canopy edge and the canopy axis. Due to such coordinate system choice it is more convenient to compute from the pole to the edge along meridional section S (from 0 to So). All values are given in dimensionless units
S = Sp/So ,  T = Tp/qS2, Rx = Rpx/So ,  r = rp/So ,  R = Rp/So ,  Dp= Dpp/q .
So is the radius of a round canopy in the plane of cutting out, index “p” means just “parachute”. Angles f, y, x and the radius curvature Rx are determined from the algebraic equations:
f = p/n, Rsin(f) = Rxsin(y), fS = yRx ,  sin(x) = sin(f)cos(q).
       The formulated one-parameter boundary value problem has been solved by Newton's method [3]. Tension value T(0) is selected on the pole so that a given value of the line length would be obtained on the canopy edge. For a numerical integration of differential equations Runge-Kutta's method of the fourth order precision [4] has been used.
       This problem was solved assuming Dp = const over the total canopy of parachute. The value of Dp for the considered parachute model with the known value of air-permeability was assigned by the constant value along the radial ribbon equal to 1.2.
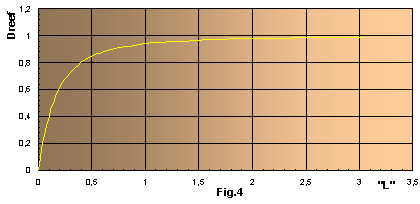
Numerical relation between D and imaginary suspension lines L
       But as the tested parachute differs essentially from the usual round parachute by its geometric parameters, then obviously, the boundary conditions (3) in view of such writing are not suitable to our variant. Knowing the exact diameter of the stripe (i.e. the reefing-line-length), tightened by a reefed cord, and taken into consideration the fact that the diameter of the stripe does not exceed f the diameter of the canopy inlet (if they are equal to each other, then short lines between the stripe and the canopy edge would be parallel to the canopy axis OQ - pole-confluence point), one may deduce the relationship between the values of the reefing D and the "imaginary" suspension lines (Fig.4):
from which one can see that D asymptotically tends to 1 (one), when L tends to infinity (that is the case when the diameter of stripe, tightened by the reefed cord, is equal to the diameter of the inlet). This relation was being put into boundary condition (3). Then the problem was being solved as if for an usual round parachute.
       The values of the drag coefficient Cp have been obtained at all values of the reefing D as a result of the numerical solution of equations taking into account the above relation - the solid curve in Fig.2. One can see that scattering between numerical and experimental data of Cp is within by 3 - 8%.
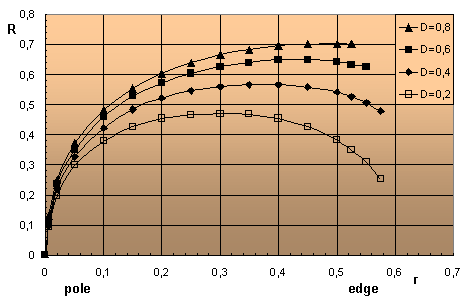
       Reefed canopy profiles obtained from the solution of the differential equations are shown in Fig.5 for parameters of the reefing 0.2 < D < 0.85 (with a step of the reefing 0.05). Having compared these profiles with photos of the corresponding canopies, one can notice their qualitative correspondence. For the quantitative comparison of experimental and numerical profiles the table of the ratio of S radial ribbon length divided by inlet radius R is shown below.
 
reef.#  D  V, m/s Snum/Rnum Sexp/Rexp  % 
1 0.40 25 2.07 2.17 4.8
2 0.50 15 1.96 1.91 3.0
3
0.55
20
1.63
1.60
1.8
4
0.60
35
1.59
1.62
1.9
5
0.70
20
1.50
1.54
3.0
6
0.75
35
1.45
1.46
0.7
7
0.80
35
1.43
1.50
4.9
9
0.95
10
1.38
1.42
2.9

       One can see from the right column that the ratio of numerical S/R to experimental, does not exceed 5%. Satisfactory agreement of the experimental and numerical values of Cp and also the shape parameters of considered parachute indicates that one may use the developed computer program.
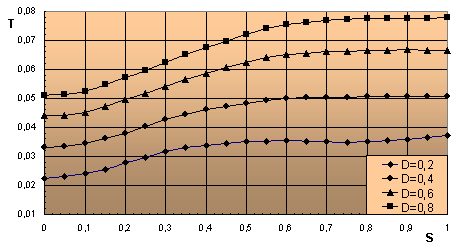
       Numerical distributions of radial ribbon tension T are shown in Fig.6 within 0.2 < D < 0.8.

Numerical profiles of parachute model at different parameters of reefing
Fig.5 Profiles of the parachute model depending on the parameters of reefing.
Numerical tension T within 0.2<D<0.8
Fig.6 Distribution of radial ribbon tension T along meridian S from the pole to the edge depending on the parameters of reefing.
CONCLUSION
As a result of experiments carrying out for the permeable  parachute model with the stripe-stabilizer at  different values of reefing and upstream flow velocities v = 10 - 35 m/s , the following is achieved: Program for computation of drag coefficient, tension of the radial ribbon and profiles of the tested parachute model has been developed. The results of computation, brought out due to this program for all values of reefing (even up to D = 0.1), are confirmed by experimental data both for Cp (a difference is 3 - 8 per cent) and for parameters of the canopy shape (a difference does not exceed 5 per cent).
 
REFERENCES
  1.  M.V. Dzhalalova, A.F. Zubkov “Numerical and Experimental Research of Permeable Parachute - SAL”, Report #4400, MSU, Institute of Mechanics,1995, p.42.
  2.  Kh.A. Rakhmatulin “Theory of Axisymmetric Parachute”, Transactions #35, Moscow State University, 1975.
  3.  B.P. Demidovich, I.A. Maron “Foundation of Computational Mathematics”, Moscow, 1960.
  4.  N.S. Bakhvalov “Numerical Methods”, Moscow, 1973.

    5. [Parachute Science]

    [home page]