
Before informing about the results of experiments it is interesting to note one fact: at first a numerical experiment has been conducted; it is discovered by preliminary results of numerical solution of a system of equilibrium differential equations for a square parachute, that the values of pressure difference for considered variants along radial ribbons are not the same. Due to this it proved necessary to conduct experiments in wind tunnel. The investigations have been carried out for two variants of a square parachute (Fig.2a, 2b). The series of experiments involved the velocity range of upstream flow from 10 to 30 m/s; line lengths varied in the typical interval for practical applicability from Lo = 2b to Lo = 4b, where b is a half of a square side.
For measurements of pressure distribution on the model surface of the square parachute the pressure sensors were installed along the shortest radial ribbon (this is the first meridional section OA1 , Fig.2a) and along the longest ribbon, which is the fourth meridional section OA4. Sorts of two fabric have been used: the first - with the air-permeability W1 = 100-300 l/m2s and another one - with W2 = 600-1000 l/m2s.
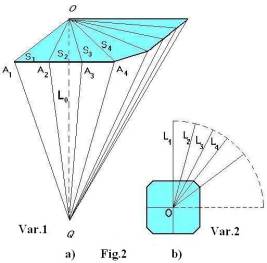
Fig.3 presents the pressure distributions along the first and fourth sections: experimental values of Dp along the first ribbon are shown by white symbols, along the fourth ribbon - by yellow ones. As one can see, the value of pressure difference along the first meridional ribbon differs very much from that along the fourth one. The values of Dp are on the ordinate axis, and S is the distance between the pole and the edge along meridian on the abscissa axis. All values are given in dimensionless units. For variant 1 with fabric permeability W2 and line lengths Lo = 2b, 3b, 4b the pressure difference along the fourth radial ribbon increases from pole to edge by 20%; along the first ribbon one can observe a quite different picture: Dp decreases from pole to edge (Fig.3). The values of Dp on the edge are less than those on the pole by 36% at Lo = 2b; by 16% - at Lo = 3b.
For the same variant 1 but with a different permeability W1 , Dp increases along the fourth section by more than 30%, but along the first section Dp decreases at first a little, then it increases.
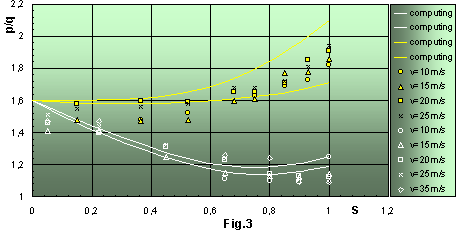
Distribution of pressure coefficient along radial ribbons of square parachute. Var.1, W2, Lo= 2b.
The parachute model for variant 2 with W2 has a quite different character of pressure distribution. Unlike variant 1, pressure difference along the fourth section strongly decreases: from pole to edge - more than three times at Lo = 2b (Fig.4); one and half times at Lo = 3b and 1.3 times at Lo = 4b. The pressure distributions along the first ribbon at all line lengths are similar: from the pole to S = 0.75 the values of Dp decrease, and from S = 0.75 to the edge they increase slightly.
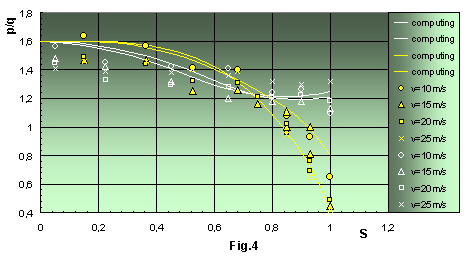
Distribution of pressure coefficient along radial ribbons of square parachute. Var.2, W2, Lo= 2b.
Thus, because of different sets
of line lengths (var.1 and var.2), a canopy of the square parachute, having
the same forms in the cutting out for both variants, attains quite different
shapes in a stream, and pressure distributions over the model of var.1
differs essentially from those for var.2. As one can see, this difference
is observed, in particular, along the fourth meridional section, that is
on the longest radial ribbon: if for var.1 Dp
increases from pole to edge, then for var.2 it decreases. The line lengths
and air-permeability effect the pressure distribution too: with increasing
the values of line length the non-uniformity of Dp
is smoothed. The pressure distributions along the first, second, third
and fourth sections are shown by solid curves, obtained from the results
of the solution of differential equations for a square parachute.
References
- M.V. Dzhalalova "Aerodynamic Characteristics of Square Parachute". MSU Bulletin (Math.& Mech.), 1983, #2, p.95-99.
- M.V. Dzhalalova, G.S.Ulianov " Experimental Investigations of Pressure Distribution over Canopy Models of Square Parachute". Report#3151, MSU, Institute of Mechanics, 1985, p.45.
- M.V. Dzhalalova, G.S.Ulianov "Differential Pressure Distribution Peculiarity over Canopy of Square Parachute". Publication: "Parachutes and Permeable Bodies", MSU Publishing, 1987, p.58-62.